傅里叶变换与频谱分析

一.傅里叶变换

https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf

https://picture.iczhiku.com/resource/eetop/wYITzKPDfJqfyMxv.pdf

用IFFT/FFT实现时的问题

Fourier_transforms_time_domain

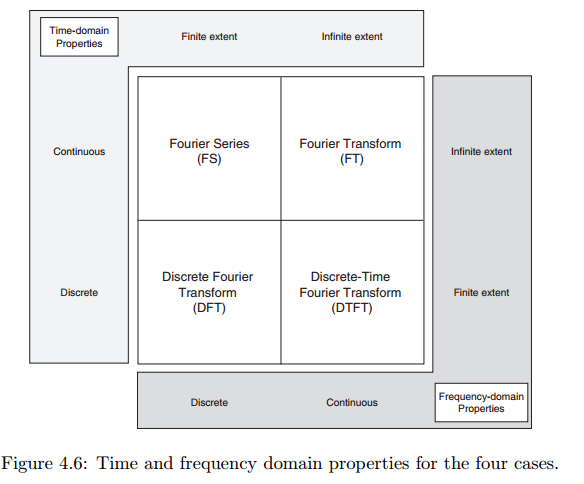
The FT is most amenable to analytical insights and manipulations, and is used in analyzing analog systems.

The DFT the workhorse that is widely used in digital computations, because of a fast algorithm called the FFT (fast Fourier transform) for computing the DFT.

Fourier_Transform_relations

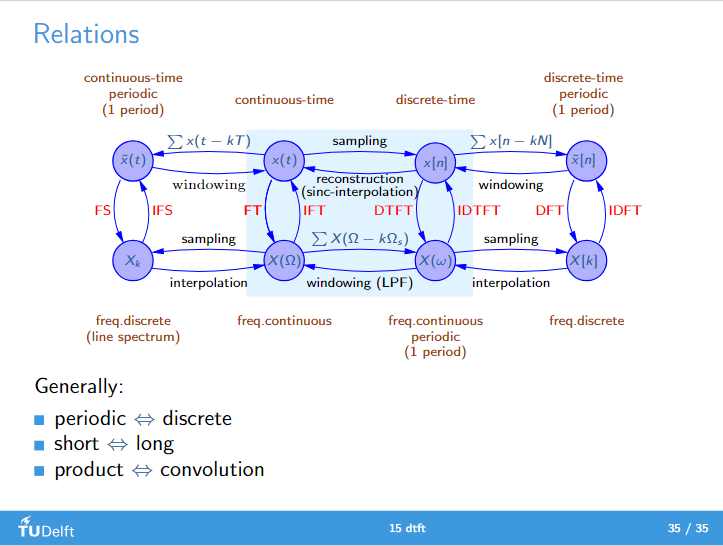
以下是连续时间和离散时间信号的傅里叶变换和逆傅里叶变换的公式，分别适用于周期信号和非周期信号。

频率f 、角频率Ω、ω

• 连续时间信号的频率表示： $\Omega$

  连续时间信号的频率范围是无限的，从负无穷到正无穷

• 离散时间的频率表示：$\omega$

  离散时间信号频率范围是有限的，从$-\pi$ 到 $\pi$。

  这个范围限制是因为离散时间信号在频域上是周期性的，主要由于采样定理的结果。一个离散信号的频谱在 $2\pi$ 的间隔内重复。

• $\Omega=2\pi f$

傅里叶变换公式

连续时间信号

连续周期信号

对于周期为 ( T ) 的连续时间信号，使用傅里叶级数（Fourier Series）表示。

• 傅里叶级数（Fourier Series）:

  $$$$

  x(t) = \sum_{k=-\infty}^{\infty} c_k e^{j \frac{2\pi k}{T} t}\ c_k = \frac{1}{T} \int_{0}^{T} x(t) e^{-j \frac{2\pi k}{T} t} dt

  $$$$

连续非周期信号

对于非周期的连续时间信号，使用傅里叶变换（Fourier Transform）表示。

• **傅里叶变换（Fourier Transform, FT）& 逆傅里叶变换（Inverse Fourier Transform, IFT） **:

  $$$$

  X(\Omega) = \int_{-\infty}^{\infty} x(t) e^{-j \Omega t} dt \ x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\Omega) e^{j \Omega t} d\Omega

  $$$$

考虑频率形式：

$$X(f) = \int_{-\infty}^{\infty} x(t) e^{-j 2\pi f t} dt \\ x(t) = \int_{-\infty}^{\infty} X(f) e^{j 2\pi f t} df$$

离散时间信号

离散周期信号

对于周期为 ( N ) 的离散时间信号，使用离散傅里叶级数（Discrete Fourier Series, DFS）表示。

• 离散傅里叶级数（DFS）:

  $$$$

  x[n] = \sum_{k=0}^{N-1} X[k] e^{j \frac{2\pi k}{N} n} \ X[k] = \frac{1}{N} \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi k}{N} n}

  $$$$

离散非周期信号

对于非周期的离散时间信号，使用离散时间傅里叶变换（Discrete-Time Fourier Transform, DTFT）表示。

• 离散时间傅里叶变换（DTFT）& 逆离散时间傅里叶变换（IDTFT):

  $$$$

  X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j \omega n} \ x[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(e^{j\omega}) e^{j \omega n} d\omega

  $$$$

考虑频率形式：

$$X(f) = \sum_{n=-\infty}^{\infty} x[n] e^{-j 2\pi f n T_s} \\ x[n] = \int_{-\infty}^{\infty} X(f) e^{j 2\pi f n T_s} df$$

对于离散时间信号$x[n]$，其频谱$X(f)$在频域中是周期性的，周期为采样频率$f_s=\frac{1}{T_s}$ 。这意味着频谱$ X(f)$在每隔$1/T_s$的频率范围内重复。

因此，分析离散时间信号的频率内容时，我们通常只需要考虑一个周期，即频率范围$[0,1/Ts]$或 $[−1/(2Ts),1/(2Ts)]$。这两种表示方法在不同文献中都有使用。

$$x[n]=x(nT_s) = \int_{0}^{1/Ts} X(f) e^{j 2\pi f n T_s} df X(f) = \sum_{n=-\infty}^{\infty} x[n] e^{-j 2\pi f n T_s}$$

二.频谱分析

1.基本频谱分析：https://ww2.mathworks.cn/help/matlab/math/basic-spectral-analysis_zh_CN.html

2.傅里叶变换：https://ww2.mathworks.cn/help/matlab/math/fourier-transforms.html

3.频谱分析：https://ww2.mathworks.cn/help/signal/spectral-analysis.html

2.1 FFT变换

对于n个均匀采样点的向量$x$，有

$$y_{k+1}=\sum^{n-1}_{j=0}w^{jk}x_{j+1},w=e^{-i\pi n}$$

上式中，$k,j$的范围为$[0,n-1]$。

数量	描述
x	采样的数据
n = length(x)	样本数量
fs	采样频率（每单位时间或空间的样本数）
dt = 1/fs	每样本的时间或空间增量
t = (0:n-1)/fs	数据的时间或空间范围
y = fft(x)	数据的离散傅里叶变换 (DFT)
abs(y)	DFT 的振幅
(abs(y).^2)/n	DFT 的幂
fs/n	频率增量
f = (0:n-1)*(fs/n)	频率范围
fs/2	奈奎斯特频率（频率范围的中点）

% 定义采样间隔 Ts=1/Fs
Ts=1/50;
%% 时域信号
%离散信号持续时间
t=0:Ts:1-Ts;% 信号持续一秒
x = sin(2*pi*15*t) + sin(2*pi*20*t);
plot(t,x)
xlabel('Time (seconds)')
ylabel('Amplitude')

%% 频域信号
y = fft(x);
Fs = 1/Ts;
f = (0:length(y)-1)*Fs/length(y);
plot(f,abs(y))
xlabel('Frequency (Hz)')
ylabel('Magnitude')
title('Magnitude')


%% 时域信号的离散傅里叶变换具有周期性，其频谱的前半部分为正频率，后半部分为负频率。
% 使用 fftshift 函数对变换执行以零为中心的循环平移。
% 双边幅度谱
n = length(x);
fshift = (-n/2:n/2-1)*(fs/n);
yshift = fftshift(y);
plot(fshift,abs(yshift))
xlabel('Frequency (Hz)')
ylabel('Magnitude')

%% 功率谱
%  双边功率谱
power = abs(y).^2/n; 
plot(fshift,power)
title('Power')
xlabel('Frequency (Hz)')
ylabel('Power')

2.2 单边和双边谱

• 单边谱：通常用于正实信号（只包含正频率）或者复信号（正频率和负频率相对称）的频域分析。单边谱可以更好地反映信号的能量分布，特别是在处理周期性或重复性的信号时。
• 双边谱：通常用于非对称的实信号或者不完全对称的复信号的频域分析。双边谱提供了完整的频域信息，包括频率和相位，适用于需要全面分析信号特性的场景。

% 创建一个离散信号  
Fs = 1000; % 采样频率  
t = 0:1/Fs:1-1/Fs; % 时间向量  
f = 5; % 信号频率  
x = cos(2*pi*f*t); % 离散信号，一个余弦波  
  
% 计算双边谱  
N = length(x); % 信号长度  
X = fft(x); % FFT计算  
P2 = abs(X/N); % 双边谱的幅度（归一化）  
P2(1) = P2(1)/2; % 直流分量需要除以2（如果其他分量是平均分配的）  
f = Fs*(0:(N/2))/N; % 频率向量（正频率部分）  
  
% 可视化双边谱  
figure;  
subplot(2,1,1);  
plot(f,P2(1:N/2+1)); % 只显示正频率部分  
title('双边谱');  
xlabel('Frequency (Hz)');  
ylabel('|P(f)|');  
  
% 计算单边谱（对于实信号，单边谱是对称的）  
P1 = P2(1:N/2+1); % 直接取双边谱的正频率部分  
  
% 可视化单边谱  
subplot(2,1,2);  
plot(f,P1);  
title('单边谱');  
xlabel('Frequency (Hz)');  
ylabel('|P(f)|');

2.3.相位谱

• 频率：表示信号中单位时间内周期性变化的次数，通常以赫兹（Hz）为单位。在数学上，频率描述的是信号中正弦波或其他周期性成分在单位时间内重复的次数。

• 相位：表示信号中某一特定时间点与参考点之间的相对位置或偏移。对于正弦波信号，相位描述了波形相对于零点的偏移量。

• 相位谱：是信号在频域中相位随频率变化的曲线，它展示了信号在不同频率下的相位信息。

  在MATLAB中，可以使用angle函数来直接获取FFT结果的相位信息。例如，如果你已经计算了$X = fft(x)$，那么相位谱$φ$可以通过$φ = angle(X)$来获取。

2.4.离散信号的频谱周期性

对于离散时间信号（即只在离散时间点上取值的信号，如数字信号），情况则有所不同。离散时间信号的频谱是周期性的，这是由离散傅里叶变换（DFT）的性质所决定的。

• 离散傅里叶变换 (DFT) 的周期性：对于一个长度为 N 的离散时间信号 x[n]，其离散傅里叶变换 X[k] 是周期为N的。即： X[k+N]=X[k],这意味着离散信号的频谱每隔 N个频率点就会重复一次。

2.5.针对CHirp信号画其频谱及分析

针对信号

$$y=exp(i\pi/4)\times e^{-i\times \frac{\pi N}{T^2}\times(t-m\frac{T}{N})^2}, 0\leq t<T$$

上式中，$m \in [0,N-1] and \in Z$

% 更加连续的信号
T=0.01;% 符号持续时间 s
N=128;% 子载波个数
%Delta_carrirer=1/(T/N);% 子载波间隔 Hz
Npoint_sig=256;% 一个符号内内采样点数
Fs_sig = Npoint_sig/(T);% 离散信号采样频率

t=0:1/Fs_sig:T-1/Fs_sig;
m=0;
y0=exp(pi/4*1i)*exp(-1i*pi*N/(T^2)*((t-m*T/N).^2));

% 仅在 T/N时采样的信号

T=0.01;% 符号持续时间 s
N=128;% 子载波个数
%Delta_carrirer=1/(T/N);% 子载波间隔 Hz
Npoint_sig=N;%一个符号内内采样点数 必须为128

Fs_sig = Npoint_sig/(T);% 离散信号采样频率
n1=0:1/Fs_sig:T-1/Fs_sig;

n1_index=n1*Fs_sig;% 索引归一化

m=0;  %  t-m*T/N
y01=exp(pi/4*1i)*exp(-1i*pi/N*(n1_index-m).^2);

T=0.01;% 符号持续时间 s
N=128;% 子载波个数
Fs_sig = 100000/(T);
t_org=0:1/Fs_sig:T-1/Fs_sig;
m=0;
y0_org=exp(pi/4*1i)*exp(-1i*pi*N/(T^2)*((t_org-m*T/N).^2));

figure;
hold on
plot(t_org,y0_org)
stem(t,real(y0))
stem(n1,real(y01))
legend('y0-org','y0','y01')
hold off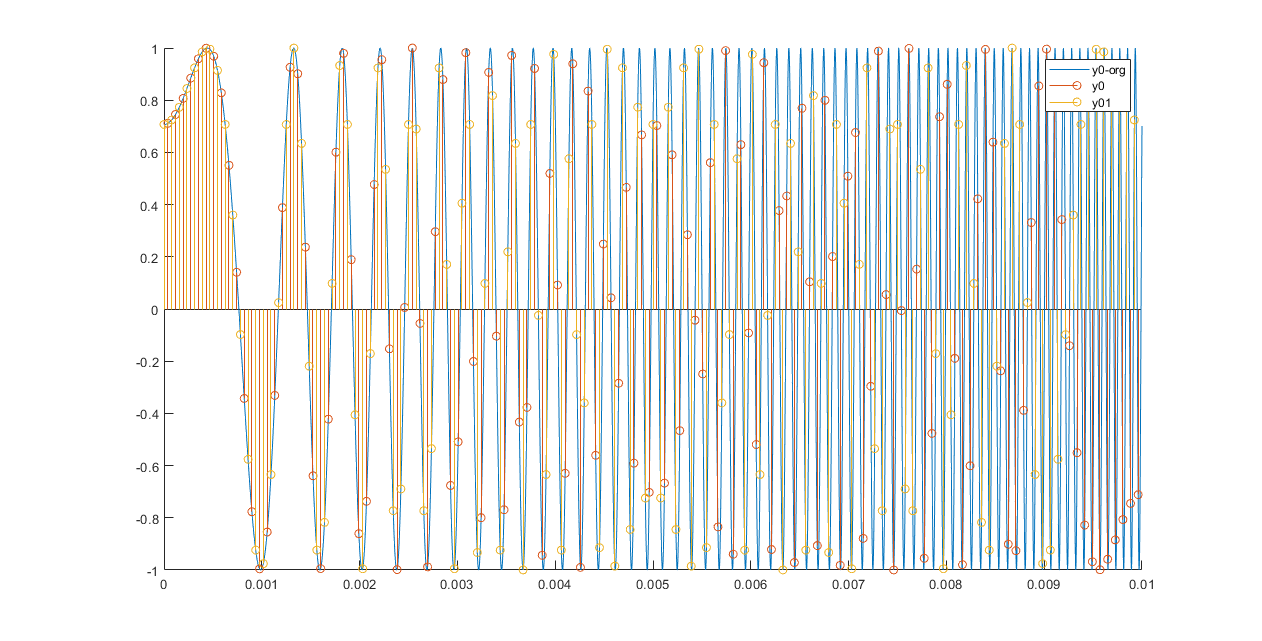

三个信号的时域图

由上图可见，y0_org,y0,y01,分别是针对信号采样点有密到稀疏。

Q：对于同一个连续信号，不同采样速率获得的离散信号，其频谱结果会不一样吗？

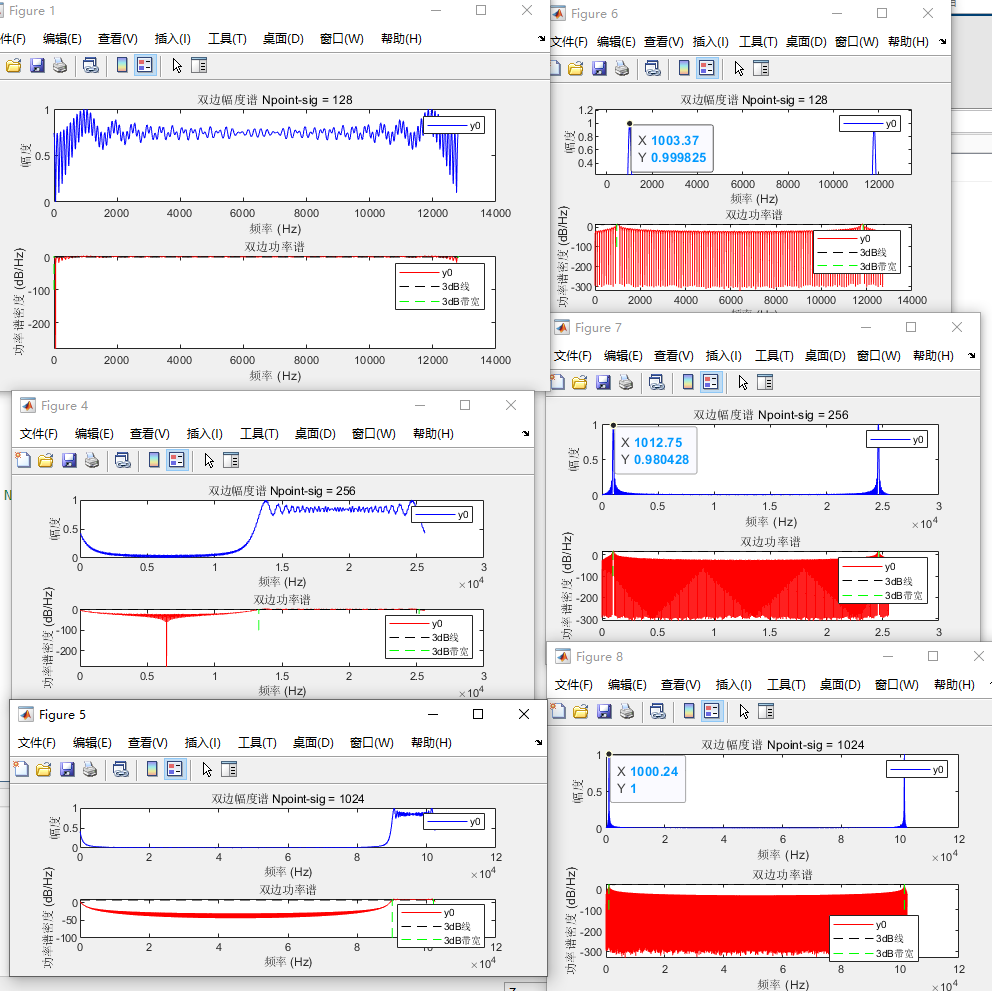
如下代码中，修改Npoint_sig值，得到的幅度谱， 信号带宽 3dB 双边谱 带宽 基本固定为11900HZ左右，但可以看到，相比于单音信号，其频谱位置在改变

这是因为 y0是一个复指数信号，其频谱特性和单音信号不同。该信号涉及一个二次相位因子，因此具有更复杂的频谱特性。更改采样点数会影响离散傅里叶变换 (DFT) 的频率分辨率和频率范围，从而影响频谱的外观。

三个信号的时域图

% 定义参数
T = 0.01; % 符号持续时间 s
N = 128; % 子载波个数
Npoint_sig = 2000; % 一个符号内内采样点数 
Fs_sig = Npoint_sig / T; % 离散信号采样频率

% 生成时间向量
t = 0:1/Fs_sig:T-1/Fs_sig;
m = 0;
y0 = exp(pi/4*1i) * exp(-1i * pi * N / (T^2) * ((t - m * T / N).^2));
% y0 = cos(2*pi*1000*t); %单音信号

% 频谱分析参数
Num_Fs_N = 4096; % 频谱分析分辨率
frequencies = linspace(0, Fs_sig, Num_Fs_N); % 调整频率范围

% 计算信号的FFT
X_f0 = fft(y0, Num_Fs_N);

% 计算功率谱
power_spectrum = abs(X_f0).^2 / length(y0);

% 计算最大功率密度
max_power = max(power_spectrum);
threshold_3dB = max_power / 2;

% 找到3dB带宽的位置
above_threshold_indices = find(power_spectrum >= threshold_3dB);
freq_3dB_start = frequencies(above_threshold_indices(1));
freq_3dB_end = frequencies(above_threshold_indices(end));

% 绘制幅度谱
figure;
subplot(2,1,1);
plot(frequencies, abs(X_f0) / max(abs(X_f0)), 'b');
title('双边幅度谱');
xlabel('频率 (Hz)');
ylabel('幅度');
legend('y0');

% 绘制功率谱
subplot(2,1,2);
plot(frequencies, 10*log10(power_spectrum), 'r');
hold on;

% 绘制3dB线
plot([frequencies(1) frequencies(end)], 10*log10([threshold_3dB threshold_3dB]), 'k--');
% 标记3dB带宽起始和结束位置
plot([freq_3dB_start freq_3dB_start], [-100 10*log10(max_power)], 'g--');
plot([freq_3dB_end freq_3dB_end], [-100 10*log10(max_power)], 'g--');

title('双边功率谱');
xlabel('频率 (Hz)');
ylabel('功率谱密度 (dB/Hz)');
legend('y0', '3dB线', '3dB带宽');

% 调整图例位置
subplot(2,1,1);
legend('Location', 'northeast');
subplot(2,1,2);
legend('Location', 'northeast');


% 输出3dB带宽信息
fprintf('3dB带宽范围：%.2f Hz 到 %.2f Hz\n', freq_3dB_start, freq_3dB_end);
fprintf('3dB带宽：%.2f Hz\n', freq_3dB_end - freq_3dB_start);