仿真-OTFS-Zak变换

1.概念

Yi Hong, Tharaj Thaj, and E. Viterbo, "Delay-Doppler Communications: Principles and Applications", AP - Elsevier, March 1st, 2022.

F. Lampel, A. Avarado and F. M. J. Willems, "On OTFS using the Discrete Zak Transform," 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Korea, Republic of, 2022, pp. 729-734, doi: 10.1109/ICCWorkshops53468.2022.9814589.

2.流程

参见：

1.https://ww2.mathworks.cn/help/comm/ug/otfs-modulation.html

2.https://github.com/DanielleJF/Zak-Transform-for-OTFS

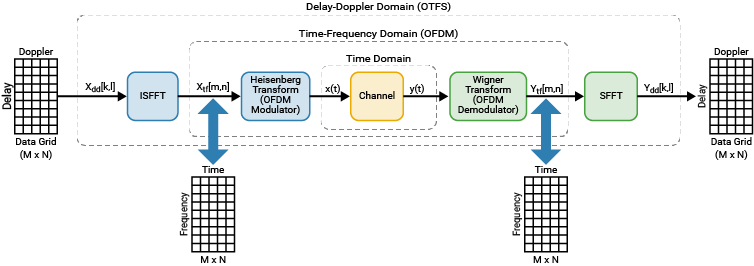
IZT变换是ISFFT和Heisenberg变换的结合体，其直接实现将时延-多普勒域上的信号映射到时域。

OTFS as a precoded OFDM system

离散傅里叶变换 DFT

设$x(n)$是一个长度为M的有限长序列，$x(n)$的N点离散傅里叶变换：

$$X(k)=DFT[x(n)]_N=\sum^{N-1}_{n=0}x(n)e^{-j\frac{2\pi}{N}kn}, \ 0\leq k\leq N-1 \\$$

N称为DFT变换区间长度，$N\geq M$

令 $W_N=e^{-j\frac{2\pi}{N}}$

傅里叶变换与逆变换对为：

$$X(k)=DFT[x(n)]=\sum^{N-1}_{n=0}x(n)W^{kn}_{N} \ ,\ 0 \leq k \leq N-1 \\ x(n)=IDFT[X(k)]=\frac{1}{N}\sum^{N-1}_{k=0}X(k)W^{-kn}_N \ , \ 0 \leq n \leq N-1$$

ISFFT+Heisenberg Transform:

$$X_{dt}=IFFT(X_{tf})=IFFT(\frac{1}{M}FFT(IFFT(X^T_{dd})^T)) \\$$

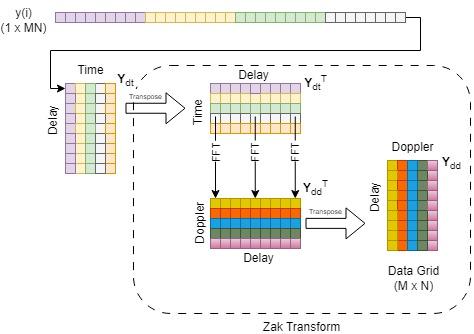
IZT:

$$X_{dt}=\frac{1}{M}IFFT(X^T_{dd})^T$$

Inverse Zak transform operation

$$x(m+nM)=vec(X_{dt}[m,n])$$

ZT:

Zak transform operation

$$Y_{dd}[m,n]=M\times FFT(Y^T_{dt})^T$$

多径效应、符号内干扰、符号间干扰ISI、ICI

关于信道G矩阵的估计：

最小化观测值$Y$（the received signal) 和 实际值$P$ (the known pilot signal)之间的均方误差，公式有：

$$\hat P =\frac{Y_{pilot}*P^*}{|P|^2+\sigma^2_n}$$

使用导频时延多普勒矩阵$\bf P_{dd}$，以估计实际的信道矩阵$\bf H_{dd}$

$$H_{dd}=\frac {Y_{dd}\times P_{dd}[1,pilotBin]^*}{|P_{dd}[1,pilotBin]|^2+n_0}$$

LMMSE信道均衡：

对于长度为MN的发送信号$x$，接收信号$y$，与之对应的信道矩阵为$G$

$$\bf y=Gx+n$$

当矩阵$G$已知，可以基于LMMSE进行信道均衡。

$$\bf \hat x=(G^HG+\sigma^2_nI_{MN})^{-1}G^Hy$$

3.导频信号与接收

3.1 定义导频符号块

对于时延-多普勒符号块 $M\times N$

定义导频矩阵为

{{\bf{P}}_{dd}}[m,n] = \left\{ {\begin{array}{*{20}{c}} {{e^{j\frac{\pi }{4}}}}&{m = 1,n = \left\lfloor {N/2} \right\rfloor + 1}\\ 0&{others} \end{array}} \right.

考虑发送数据结构：

导频符号块+数据符号块+数据符号块+...

即导频估计的信道信息，认为在后续的若干个数据符号块是不变的，可以直接使用，用以均衡。

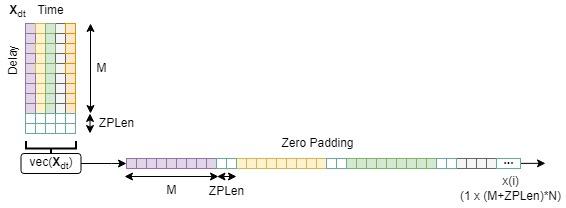
3.2 ZP-OTFS

Zero padding operation

3.3 定义时延多普勒信道

略

采样率为fsamp的OTFS调制发送信号，经过多径多普勒信道后，得到的接收信号为

Zak_Receive_signal

3.4 获得采样窗的信号

观察程序，这里截取的直接是如下

image-20240626174948281

经代码仿真测试，当窗往后移动，则性能会变差。

这要求OTFS帧同步必须要抓到第一径的信号

2.4 获取对$\mathbf{H}_{dd}$的估计

对接收到的导频帧进行IZT，并利用LMMSE估计，得到$\mathbf{H}_{dd}$

center_row = 1; % 行代表时延，时延只会是非负整数
center_col = ceil(N/2);% 列代表多普勒，多普勒可以有正负，用中间标志 “0中频”？

[lp,vp] = find(abs(Hdd) >= 0.05);
chanEst.pathGains = diag(Hdd(lp,vp));   % get path gains
chanEst.pathDelays = lp - center_row;            % get delay indices
chanEst.pathDopplers = vp - center_col;   % get Doppler indices