理论与仿真-OTFS 同步

Mr.Wenxin2025年4月1日大约 17 分钟

理论与仿真-OTFS 同步

一、[调研]相关论文：

中文：

陈杨,杨海艳,程恺英,刘恒,马征.基于时延-多普勒域信号稀疏性的OTFS帧同步算法[J/OL].电信科学:1-20[2024-05-28 09:03].
廖勇, 罗渝, 荆亚昊. 6G新型时延多普勒通信范式：OTFS的技术优势、设计挑战、应用与前景[J]. 电子与信息学报. doi: 10.11999/JEIT231133

OTFS中通常涉及帧同步、符号同步、载波同步和时频同步。

帧同步确保接收端能够正确识别和解码每个数据帧的起始位置的问题。由于信号可能经历多路径传播和多普勒效应，因此需要帧同步来确保接收端准确地找到数据帧的边界。
符号同步涉及确保接收端能够正确识别和解码每个符号或数据块的时间定时问题。

在OTFS系统中，信号的时域特性可能会导致符号定时偏移，因此需要符号同步来校正这种偏移，以确保正确解码数据。载波同步是确保接收端能够正确识别和解码信号的载波频率的问题。

由于OTFS系统中信号的频域特性可能受到多普勒效应的影响，因此需要载波同步来校正载波频率偏移，以确保正确解调信号。时频同步涉及在OTFS系统中同时校正时间偏移和载波频率偏移，以确保接收端在时域和频域上与发送端保持一致。

二、定时同步

参阅文章：王皓星.宽带无线传输系统中同步技术研究与FPGA实现[D].西安电子科技大学.2022.

在OFDM中，有：

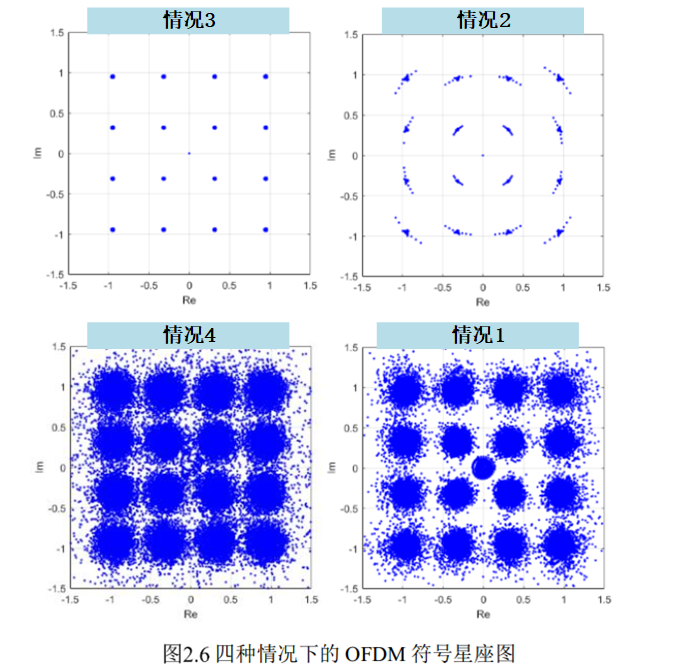
如上图：

情况1：符号同步估计位置大幅度提前，落在循环前缀之前。
数学推导类似情况4，存在ISI影响，子载波之间正交性被破坏。
情况2：符号同步估计位置较为提前，但仍落在信号帧的CP之中。这种情况下进行 FFT解调时，信号帧相当于进行了循环移位。
发射端的信号帧为 $x(n),n=0,1,2,\cdots,N-1$ ，接收端的符号同步估计误差为 $\delta$ ，则对应的接收信号为 $y(n)=x(n-\delta)$ ，将 $y(n)$ 进行FFT变换得：
$\begin{array}{l} Y(k) = FFT(y(n))\\ = FFT(x(n - \delta ))\\ = \frac{1}{{\sqrt N }}\sum\limits_{n = 0}^{N - 1} {x(n - \delta )\exp ( - j\frac{{2\pi kn}}{N})} \\ = \frac{1}{{\sqrt N }}\sum\limits_{l = - \delta }^{N - 1 - \delta } {x(l)\exp ( - j\frac{{2\pi k(l + \delta )}}{N})} \end{array}$
根据循环前缀的特点与FFT循环移位性质可得：
$\sum\limits_{l = - \delta }^{ - 1} {x(l)\exp ( - j\frac{{2\pi k(l + \delta )}}{N})} = \sum\limits_{l = N - \delta }^{N - 1} {x(l)\exp ( - j\frac{{2\pi k(l + \delta )}}{N})}$
则可以推出
$\begin{array}{l} Y(k) = \frac{1}{{\sqrt N }}\sum\limits_{l = 0}^{N - 1} {x(l)\exp ( - j\frac{{2\pi (l + \delta )}}{N}k)} = X(k)\frac{1}{{\sqrt N }}\exp ( - j\frac{{2\pi \delta }}{N}k)\\ X(k) = \frac{1}{{\sqrt N }}\sum\limits_{l = 0}^{N - 1} {x(l)\exp ( - j\frac{{2\pi l}}{N}k)} \end{array}$
当符号同步估计位置在 CP 之中时，子载波之间的正交性不会被破坏，且信号帧经过 FFT 变换后得到的数据的相位会发生旋转。数据的相位旋转可以在信道估计与均衡模块进行相位纠正。所以，符号同步的估计结果应尽量落在循环前缀中。
情况3：符号同步估计位置与实际位置一致，FFT解调时不会受到ISI与ICI
情况4：符号同步估计位置滞后，落在信号帧的数据中。
FFT 窗口除了会包含本信号帧的数据 $x(n)$ ，也会包含一些与本信号帧无关的数据 $w(n)$ ,接收端同步估计误差依旧记为 $\delta$ ，则接收信号可表示为
$y(n) = x(n + \delta ),0 \le n \le N - 1 - \delta ;w(n),N - \delta \le n \le N - 1$
进行FFT变换结果有：
$\begin{array}{c} Y(k) = \frac{1}{{\sqrt N }}(\sum\limits_{n = 0}^{N - 1 - \delta } {x(n + \delta )\exp ( - j\frac{{2\pi kn}}{N})} + \sum\limits_{n = N - \delta }^{N - 1} {w(n)\exp ( - j\frac{{2\pi kn}}{N})} )\\ = \cdots \cdots \\ = X(k)\exp (j\frac{{2\pi k\delta }}{N})\frac{{N - \delta }}{N}\frac{1}{{\sqrt N }} + ISI \end{array}$
数据发生相位旋转和幅度变化，而且引入ISI，破坏了子载波间的正交性。
最终使得解调后的星座图会发生弥散，导致OFDM系统传输性能大幅度下降。

三、[算法] 定时同步

3.0 核心问题

定时同步性能如何分析？
粗同步和细同步是什么？
误差如何分析？
通信的同步算法中，如何解决因多普勒频偏带来的相关峰值变化问题

3.1 OFDM-基础S&C

参阅：https://www.cnblogs.com/jiandahao/p/9310924.html

3.2 OFDM-改进S&C

3.3 PMF-FFT算法

参阅：万新杰.高动态短猝发信号接收关键技术研究与FPGA实现[D].西安电子科技大学.2017.
刘畅. 高速移动多模式扩频通信系统物理层设计与实现[D].电子科技大学,2023.DOI:10.27005/d.cnki.gdzku.2022.003268.

简要说明

针对 1x2048的OTFS时域符号块（32x64)，单独使用一个OTFS符号块用一实现PMF-FFT算法

帧结构：
看作前后两段896点的伪随机序列，外加2x128的间隔，后跟实际数据块
PMF-FFT导频块示意图

1.OTFS参数说明：

类比OFDM，OTFS符号块 $N\times M$ 可以看作是OFDM符号块 $N\times 1$ 在每个点上进一步细分

考虑子载波间隔为 $\Delta f$ ,OTFS符号的时间为 $T$ ，则有

T_{symbolBlock}=N\times T=\frac{N}{\Delta f}

OTFS采用索引来表示多普勒和时延，其相应

多普勒分辨率: $ \Delta f/(N)$

时延分辨率(也即离散样点时间间隔）： $T_s=T/M$

2.PMF-FFT算法说明：

针对每一段同步序列，采用分段求和计算同本地序列的相关值，记其分段数为 $P$ ， $W$ 为每段的长度， $T_c$ 为码片时间。

在这里，我们认为 $T_c=T/M=1/(M\Delta f)$

频偏估计分辨率为： $\frac{1}{{N_{fft}W{T_c}}} = \frac{M\Delta f}{N_{fft}W}$

频偏估计范围： $\frac{M\Delta f}{N_{fft}W}\times[-\frac{N_{fft}}{2},\frac{N_{fft}}{2}-1]$

此范围内，保证了定时同步估计的同时，且频偏估计值唯一

3.使用PMF-FFT算法进行OTFS的定时同步以及频偏估计时

考虑单路径
- 仅考虑定时同步
  - 多普勒频偏允许范围为 $\frac{M\Delta f}{N_{fft}W}\times[-N_{fft},N_{fft}-1]$
    超过这个范围，存在完全抓不到同步峰的情况

4.不采用归一化处理时的相关值波动问题

这里存在两个影响因素

信道的复增益
- 复增益的巨大变化，会带来相关峰值的巨大变动
信号的多普勒频偏
- 多普勒频偏的增大，伴随着相关峰值的衰减

参数配置：
OTFS N=32 M=64 W=128 N_fft=8
OTFS 多普勒分辨率为 DeltaF/2048   PMF-FFT分辨率为 DeltaF/896
考虑单路径 时延索引取0 ，多普勒频偏取 可估计范围[-DeltaF/256,DeltaF/256-DeltaF/896]内 
即索引值可取 [-3,2] 仍在可估计范围内
信噪比设置为14 dB

目的：观察 不同多普勒频偏下的相关峰值，看其波动是否较大

由下图可见，当多普勒频移值较大时，不经归一化处理，相关峰值波动较大，不容易确定门限

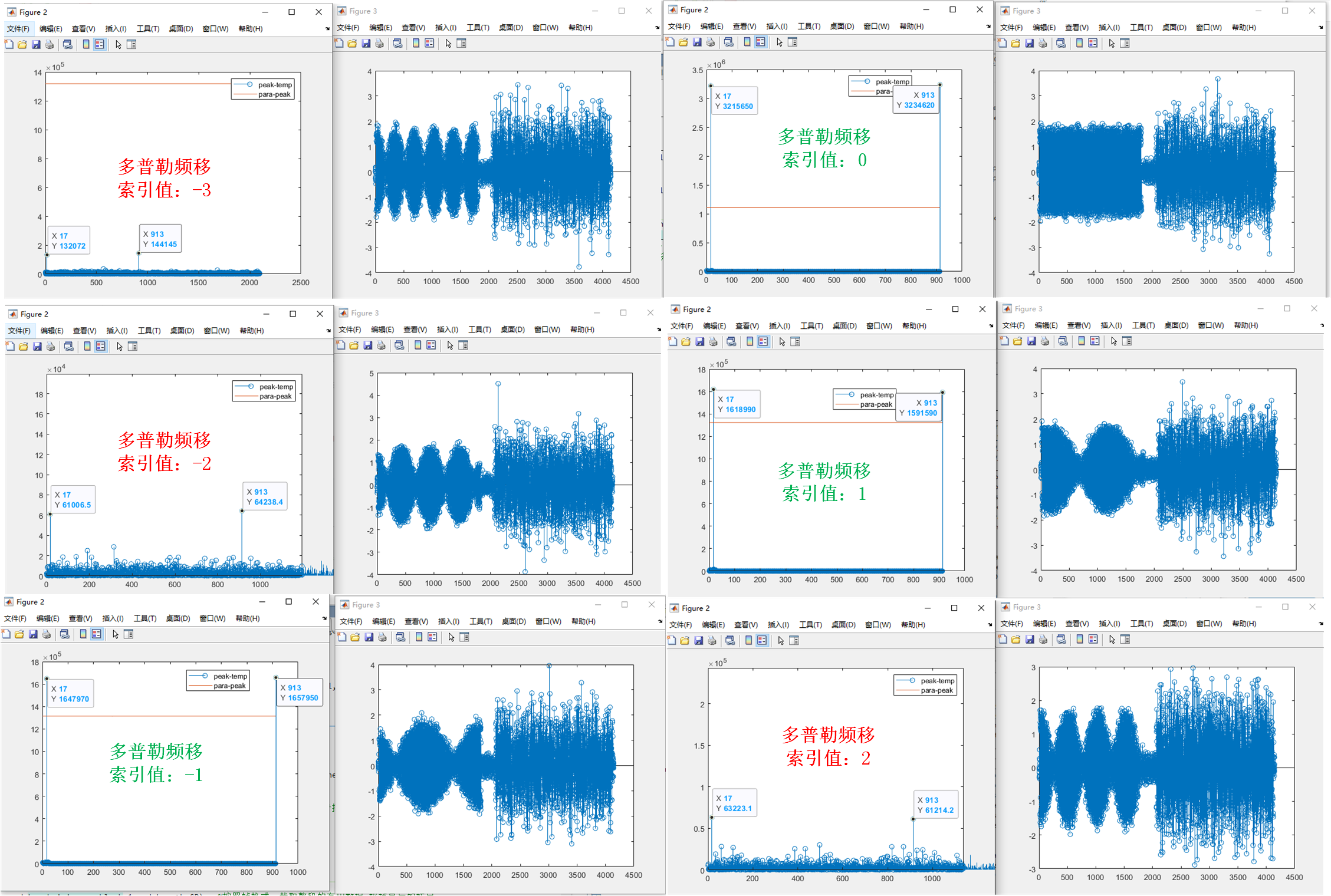
详细分析

|y(x)| = \left| \frac{\sin(\pi f X T_c)}{\sin(\pi f T_c)} \right| \cdot \left| \frac{\sin(P \pi (X T_c f - x))}{\sin(\pi (X T_c f - x))} \right|

上式中 $x=\frac{k}{N}$

对于第一项，可以看作函数 $y=abs(sin(nx)/sin(x))$

%%
% 定义n的值  
n = 5;  
  
% 定义x的范围，避开x=k*pi（k为整数）的点  
x = linspace(-pi + eps, pi - eps, 1000);  
  
% 初始化y的数组  
y = zeros(size(x));  
  
% 计算y的值，同时处理sin(x)接近零的情况  
idx = abs(sin(x)) > eps;  
y(idx) = abs(sin(n*x(idx)) ./ sin(x(idx)));  
  
% 绘制函数图像  
figure;  
plot(x, y);  
title(['y = abs(sin(' num2str(n) 'x) / sin(x))']);  
xlabel('x');  
ylabel('y');  
grid on;  
axis([-pi pi 0 max(y) + 0.1*max(y)]); % 设置坐标轴范围以更好地显示图形  
  
% 在x=-pi/n和x=pi/n处绘制垂直参考线  
hold on;  
plot([-pi/n, -pi/n], [0, max(y) + 0.1*max(y)], 'k--'); % x=-pi/n的垂直线  
plot([pi/n, pi/n], [0, max(y) + 0.1*max(y)], 'k--');   % x=pi/n的垂直线  
  
% 添加文本标签说明这两个点  
text(-pi/n, max(y) + 0.05*max(y), '-\pi/n', 'HorizontalAlignment', 'center');  
text(pi/n, max(y) + 0.05*max(y), '\pi/n', 'HorizontalAlignment', 'center');  
  
hold off;

有：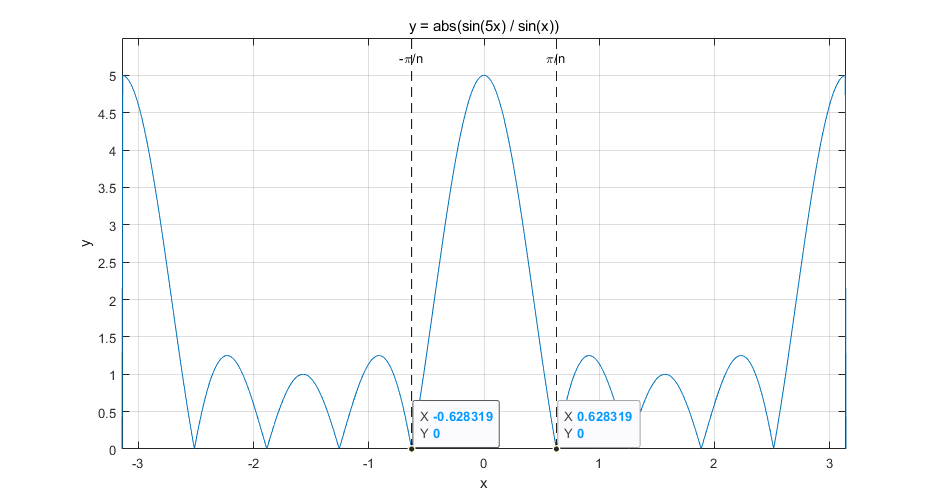

第二项类似于第一项，存在偏移。

%%
% 常参数  
X = 32; %同步序列分段序列长度 
delta_f=60*10e3;% Hz
Tc = 1/delta_f; % 符号持续时间 
P = 32; % PMF-FFT点数
PMF_FFT_resolution_ratio=delta_f/(P*X);% Hz


% x的范围，确保不覆盖会导致分母为零的点  
N=P*1000;
x_range = (-N:N-1) / N;    
% 初始化y向量  
y = zeros(size(x_range));  
index_doppler=(-5:1:5);
Doppler_select=1*PMF_FFT_resolution_ratio*index_doppler;

y_result=zeros(length(Doppler_select),length(x_range));

for j=1:length(Doppler_select)
    f=Doppler_select(j);
    if f==0
        f = 1; % 多普勒频偏值，这里视其为无频偏 ,函数限制取f=0
    end
% 计算y的值，同时避免除以零  
for i = 1:length(x_range)  
    x = x_range(i);  
      
    % 避免分母为零  
    if abs(sin(pi*f*Tc)) > eps && abs(sin(pi*(X*Tc*f-x))) > eps  
        y_result(j,i) = abs(sin(pi*f*X*Tc) / sin(pi*f*Tc)) * abs(sin(P*pi*(X*Tc*f-x)) / sin(pi*(X*Tc*f-x)));  
    else  
        % 在分母为零的点，可以设置一个默认值，比如0或者NaN  
        y_result(j,i) = NaN; % 或者 y(i) = 0; 如果你想要在这些点上取0值  
    end  
end
end
  
% 绘制图像 
figure;
hold on
 
% 循环绘制曲线并找到每条曲线的最大值  
for j = 1:size(y_result, 1)  
    % 绘制曲线  
    plot(-N:N-1, y_result(j,:), 'DisplayName', num2str(index_doppler(j)));  
      
    % 找到当前曲线的最大值及其索引  
    [maxValue, maxIndex] = max(y_result(j,:));  
      
    % 转换索引为 x 坐标值（如果 x 是从 -N 到 N-1 的连续值）  
    maxX = -N + maxIndex;  
      
    % 使用scatter函数在图上标出最大值，使用红色圆点  
    scatter(maxX, maxValue, 'r', 'filled');  
       
end  
  
% 添加图例（如果 index_doppler 包含有意义的标签）  
if ~isempty(index_doppler)  
    legend('show'); % 显示带有 'DisplayName' 的图例  
end 
hold off
xlabel('x');  
ylabel('|y(x)|');  
title('Plot of |y(x)|');  
grid on;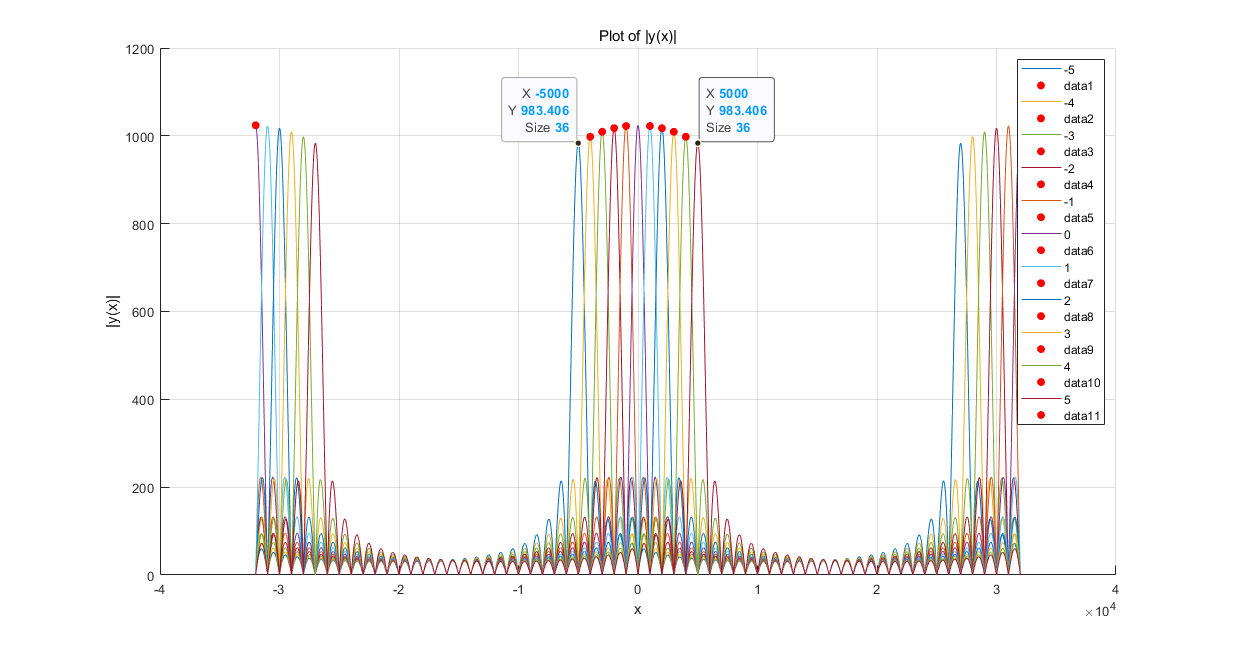

观察下图，频偏索引等于 -1 和频偏索引等于 +31 的两条函数曲线

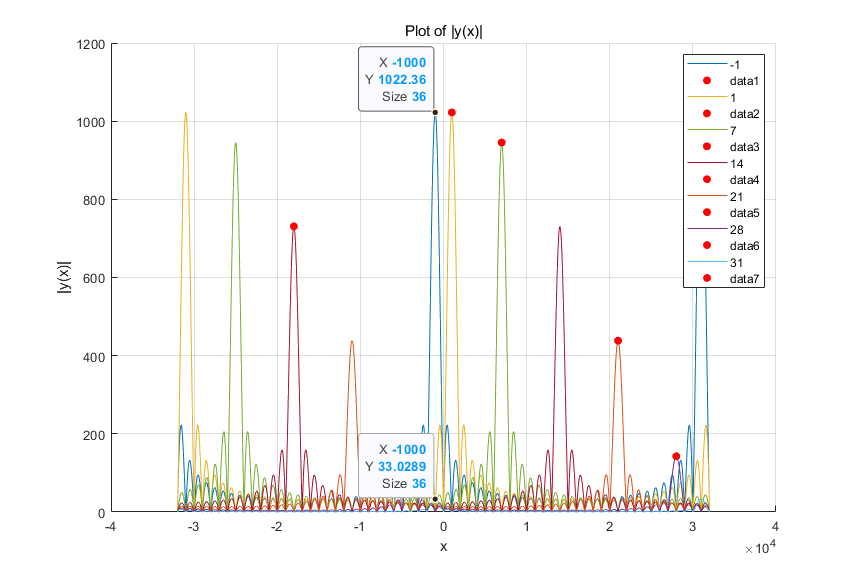
可以发现，频偏等于 +31的项，其函数峰值很小，同时和频偏等于-1的项冲突，存在于同一个位置。

故而PMF-FFT算法，当子载波间隔为 $\Delta f=Tc$ 码元持续时间，采用 $N_{fft}$ 点进行估计频偏位置时，其可估计的频偏范围为 $[-N_{fft}/2,N_{fft}/2-1]*\Delta f$ 。

3.3.1 频偏分辨率及最大值

根据PMF-FFT算法，记其分段数为 $P$ ， $W$ 为每段的长度， $T_c$ 为码片时间，有 $T_c=1/R_b$ 。

当利用最大FFT值 $\mathop {\max }\limits_k |X(k)|$ 确定k值，利用 $f_d=\frac{k}{N_{fft}WT_c}$ 来估计当前的频偏 $f$ ，则频偏分辨率为

\frac{1}{{N_{fft}W{T_c}}} = \frac{1}{{8 \times 128 \times {T_c}}}

考虑OTFS发送的时域信号(NXM)，假设离散点之间的时间间隔为 $T_s$ ,OTFS符号的时间为 $T$ ,子载波间隔为 $\Delta f$ ,

对于OTFS, $T_{frame}=NT=NMT_s,T=1/\Delta f$

$T_c=T/M$

PMF-FFT的分辨率为 $\frac{1}{N_{fft}WT_c}=\frac{M\Delta f }{N_{fft}W}$

转为时域串行序列后，OTFS多普勒分辨率为

\frac {1}{NT}=\frac{\Delta f}{N}

对于 $N_{fft}=8,W=128,N=32$

有PMF-FFT分辨率为 $64\Delta f /896$ ，OTFS分辨率为 $\Delta f /32$

频偏估计范围

当利用最大FFT值 $\mathop {\max }\limits_k |X(k)|$ 确定k值，利用 $f_d=\frac{k}{N_{fft}WT_c}$ 来估计当前的频偏 $f$ ，即确定k的取值

k的取值范围为 $[0,N_{fft}-1]$

则可以估计的频偏可近似看作

[-\frac{1}{WT_c},\frac{1}{WT_c}]=[-\frac{M\Delta f}{W},\frac{M\Delta f}{W}]

实际仍比这个值小，无法到达上界: 到达上界则为0，实际就是要小

3.3.2 归一化相关峰值

步骤1：计算相关值

首先，计算接收信号和训练序列的相关值。对于接收信号 ( r[k] ) 和训练序列 ( s[k] )，其相关值可以定义为：

\text{Correlation} = \sum_{k=1}^N r[k] \cdot s[k]^*

其中 ( N ) 是训练序列的长度， ( * ) 表示复共轭。

步骤2：归一化相关值

归一化相关值的计算公式为：

\text{NCP} = \frac{|\sum_{k=1}^N r[k] \cdot s[k]^*|}{\sqrt{\sum_{k=1}^N |r[k]|^2 \cdot \sum_{k=1}^N |s[k]|^2}}

即将相关值的绝对值除以接收信号和训练序列的能量的平方根，从而实现归一化。

3.3.3 动态门限-计算峰值系数

最佳判决门限是相对于一个固定的输入信号功率而言的，而在本文所研究的通信场景下，接收端输入信号的功率波动较大，进而导致用于判决的相关峰值也有较大的波动

P_A=\frac{P_s \cdot c}{P_r}

上式中， $P_{A}$ 是峰值系数， $P_s$ 为接收端输入信号的20000个样点的平均幅值，c为常系数。

3.3.4 问题

当频偏超过了估计范围，会出现什么情况？
动态门限和归一化峰值的作用分别是什么？

3.3.5 整数多普勒频偏与频偏位置估计

********************************
% 单条路径
PMF-FFT同步序列分段数: 28分段同步序列点数 28 PMF-FFT点数 32    归一化门限判决系数
记子载波间隔为X，PMF-FFT分辨率为 : M*X/(N_fft*分段同步序列点数) : (64X)/(32*28)   OTFS分辨率为 X/(N) : X/32
********************************

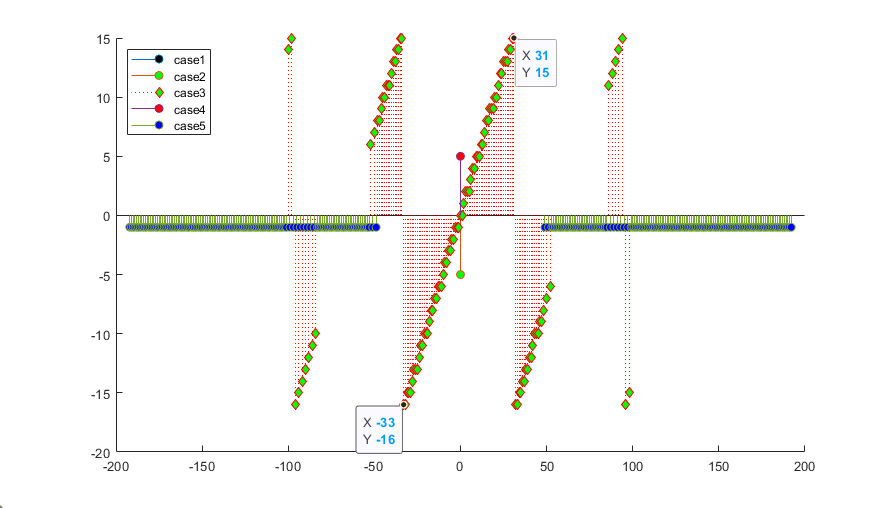
可见，当多普勒频偏落在PMF可估计的范围内时，针对单条路径，可以完成定时同步，频偏估计值唯一；但当多普勒频偏超过了可估计的范围时，则频偏估计便不为一了。

此外，随着多普勒频偏超过范围，即便仅考虑定时同步，也存在完全抓不到相关峰的情况，其原因推测

1.多普勒频偏较大，使得归一化的门限设置为0.2不行
- 相关损失：PMF-FFT的归一化相关峰值会随多普勒频偏的增加，整体呈现衰减趋势
- 扇贝损失：归一化相关峰值在某些频点上出现了衰落现象是FFT的频谱分辨率有限导致的。
2.当超过了频偏估计范围后，虽然存在某些仍然可以定时同步，但根据上图，存在某些未知情况，即超过范围后不可信。

四、[仿真]信道建模

4.1 莱斯及瑞利信道

概念参考：https://mp.weixin.qq.com/s/orFwKJ70UooKYXTvh9vv3A

switch type
    case 0
        %%%%%%%%%%%%%%%莱斯信道-begin%%%%%%%%%%%%%%%%%%%%%%%%%%
        %K : 莱斯因子，表示直射路径与多径的功率比
        num_multipath = taps-1; % 次要路径数量
        % 计算直射路径和多径的总功率
        %total_power = 1; % 假设总功率为1，用于归一化
        main_path_power = K / (K + 1); % 直射路径功率
        multipath_power = 1 - main_path_power; % 多径的总功率
        % 直射路径增益（归一化到主路径功率）
        main_path_gain = sqrt(main_path_power); % 取平方根以得到幅度
        % 模拟次要路径的增益（瑞利分布），并缩放以匹配总的多径功率
        multipath_gains = (randn(1, num_multipath) + 1i*randn(1, num_multipath))./sqrt(2);
        multipath_total_gain = multipath_gains / sqrt(sum(abs(multipath_gains).^2)); % 归一化多径增益
        multipath_gains_scaled = multipath_total_gain * sqrt(multipath_power); % 缩放以匹配总的多径功率
        chan_coef=[main_path_gain,multipath_gains_scaled];
        %%%%%%%%%%%%%%%莱斯信道-end%%%%%%%%%%%%%%%%%%%%%%%%%%
    case 1
        %%%%%%%%%%%%%%%瑞利信道-begin%%%%%%%%%%%%%%%%%%%%%%%%%%
        multipath_gains = (randn(1, taps) + 1i*randn(1, taps))./sqrt(2);
        multipath_total_gain = multipath_gains / sqrt(sum(abs(multipath_gains).^2)); % 归一化多径增益
        %%%%%%%%%%%%%%%瑞利信道-end%%%%%%%%%%%%%%%%%%%%%%%%%%
end

4.2 NTN-TDL

参阅：https://hscc.csie.ncu.edu.tw/38811.pdf
https://www.uiy.com/cn/News/5G_NTN_the_Revolution_of_Mobile_Communication/

非地面网络（Non-Terrestrial Network, NTN)中基于抽头延迟线（Tapped Delay Line）的NTN-TDL信道模型。

The Doppler shift and Doppler variation depend on the relative speed of the space/airborne platforms, the speed of the UE (User Equipment) , and the carrier frequency.

表格 RMS时延扩站和K因子：

频段	S频段	2~4 GHz	Ka频段	26.5~40Ghz
路径条件	LOS	NLOS	LOS	NLOS
RMS时延扩展（均值-对数）	-7.73	-7.74	-8.02	-7.21
RMS时延扩展（均值-s）	1.8621e-08	3.8905e-08	9.5499e-09	6.1660e-08
时延扩展对应的路径光速(3x1e8)xRMS m	5.5863	11.6715	2.8650	18.4980
RMS时延扩展（方差-对数）	0.66	0.49	0.72	0.56
K因子（dB）	7.9		10.3
K因子功率比值（无系数）	6.1660		10.7152

RMS时延扩展定义为最大传输时延和最小传输时延的均方根差值，即所有可分辨时延信号与平均时延之差的平方的平均值的平方根。以下是使用Markdown格式重新表述的RMS时延扩展的数学计算表达式，以确保它在大多数平台上都能正确显示：
RMS时延扩展（Root Mean Square Delay Spread）的数学计算表达式为：
首先，计算所有路径时延的平均值：
$\bar{\tau} = \frac{1}{L} \sum_{i=0}^{L-1} \tau_i$
其中，(L) 是多径的数量，( $\tau_i$ ) 是第 $i$ 条路径的时延。
接着，计算时延的均方值：
$\sigma_{\tau}^2 = \frac{1}{L} \sum_{i=0}^{L-1} (\tau_i - \bar{\tau})^2$
最后，RMS时延扩展是时延均方值的平方根：
$\text{RMS Delay Spread} = \sqrt{\sigma_{\tau}^2}$
采用对数形式表示（ $log_{10}(DS/1s)$
$\text{Logarithmic RMS Delay Spread (dB)} = \log_{10}\left(\frac{\text{RMS Delay Spread}}{1 \text{ second}}\right)$
注意，这里的对数形式是以分贝（dB）为单位的，它表示RMS时延扩展相对于1秒这个参考值的比例（以10为底的对数）。当RMS时延扩展小于1秒时，这个对数形式的值将是负数；当RMS时延扩展大于1秒时，这个值将是正数。这样，我们就可以通过查看这个对数形式的值来直观地了解RMS时延扩展的严重程度。

存在主路径时，存在K因子

K = 直射分量功率 / 多径分量功率

K_{\text{dB}} = 10 \log_{10}\left(\frac{P_{\text{LOS}}}{P_{\text{MP}}}\right)

4.2.1 Ka频段 NLOS信道模型仿真

OTFS N=32 M=64，子载波间隔为：60kHz,单个多普勒抽头对应1.875kHz

PMF-FFT 同步序列长度896点，N_fft=8 W=128 分段数=7

载波频率 $f_c=20 GHz$

RMS(对数）=-6.65 / 即 2.2387e-07 s

路径	归一化时延	真实时延 s	功率	衰落分布
1	0	0	0	Rayleigh
2	0.7249	1.622848953348188e-07	-1.973	Rayleigh
3	0.7410	1.658892363679138e-07	-4.332	Rayleigh
4	5.7392	1.284846835847140e-06	-11.914	Rayleigh

l落在OTFS网格上时，真实时延为(s）：0 2.6042e-07 2.6042e-07 1.3021e-06

卫星和无人机通信(仰角为40°），认为LEO的多普勒频偏主要由终端运动决定。（卫星由于其运行轨道确定，对其多普勒采用预补偿）

终端移动速度：500km/h=138.8889 m/s

**最大多普勒频移：6.694 KHz **

Doppler_vel = (max_UE_speed*car_fre)*(6370*10^3+35800*10^3)*sind(40)/(299792458)/sqrt(2*6370*10^3*(6370*10^3+35800*10^3)*(1-cosd(40))+(35800*10^3)^2);

故而多普勒索引值取值[-4,4]，随机产生四条路径的多普勒频偏

PMF-FFT仿真结果

% 20240620_180950.txt
仿真说明：使用analysis_240617.m 脚本,,同步算法为 PMF-FFT归一化判决门限为0.2
***********
仿真参数配置:
{"SNR_dB":[10,11,12,13,14,15,16,17,18,19,20],"N_fram":20000}
{"SNR_dB":[10,11,12,13,14,15,16,17,18,19,20],"N_fram":20000}
***********
同步捕获结果:
{"case1":[0,0,0,0,0,0,0,0,0,0,0],"case2":[10419,10196,10451,10372,10294,10265,10397,10348,10362,10454,10440],"case3":[9578,9801,9548,9628,9704,9730,9599,9651,9637,9544,9560],"case4":[0,0,0,0,0,0,0,0,0,0,0],"case5":[3,3,1,0,2,5,4,1,1,2,0]}

改进S&C算法 [B,CP,A,A]

% 算法参数配置
*** length_B=64 length_CP=16
length_A=256;
PARA_Train_seq.L = 64;%ZL序列长度
PARA_Train_seq.Lr = 3;%ZL序列r值
PARA_Train_seq.b = 64;%Zb序列长度
PARA_Train_seq.br = 9;%Zb序列r值
PARA_Train_seq.c = 96;%Zc序列长度
PARA_Train_seq.cr = 7;%Zc序列r值

改进S&C算法仿真结果

% 20240621_115125.txt
仿真说明：使用analysis_240617.m 脚本, 同步算法为  xie-S&C-improved
***********
仿真参数配置:
{"SNR_dB":[10,11,12,13,14,15,16,17,18,19,20],"N_fram":20000}
{"SNR_dB":[10,11,12,13,14,15,16,17,18,19,20],"N_fram":20000}
***********
同步捕获结果:
{"case1":[5,10,9,9,9,13,7,18,11,13,9],"case2":[8168,8281,8540,8718,8794,8950,9145,8993,9187,9280,9184],"case3":[8243,8586,8494,8682,8961,8892,8843,9072,9029,9057,9160],"case4":[166,220,280,356,441,579,701,838,972,1054,1213],"case5":[3418,2903,2677,2235,1795,1566,1304,1079,801,596,434]

4.3 卫星通信信道模型

matlab工具箱：https://ww2.mathworks.cn/help/satcom/getting-started-with-satellite-communications-toolbox.html

贡献者

happy-cmd