01.电路
01.电路
以下内容总结自 《电路基础(第三版》教学指导书 王松林 王辉 编著
为个人学习笔记记录,学习使用
一、电路的基本规律
基尔霍夫定律(KL)
电流定律 KCL
对于集中参数电路中的任一节点(或广义节点),在任一时刻,流出(或流入)该节点的所有支路电流的代数和等于0
电荷守恒原理
电压定律 KVL
对于集中参数电路中的任一回路,在任一时刻,沿回路指定的绕行方向,所有支路电压的代数和等于0
能量守恒原理
受控电压源、受控电流源
理想运放
运算放大器(英语:Operational Amplifier,缩写:op amp或opamp),简称运放,是一种直流耦合,差模(差动模式)输入、通常为单端输出(Differential-in, single-ended output) 的高增益(gain)电压放大器。运算放大器能产生一个比输入端电势差大数十万倍的输出电势(对地而言)。[2]因为刚开始主要用于加法,减法等模拟运算电路中,因而得名。
https://wuhongyi.cn/HardwareNote/Preamplifier/OperationalAmplifier.html
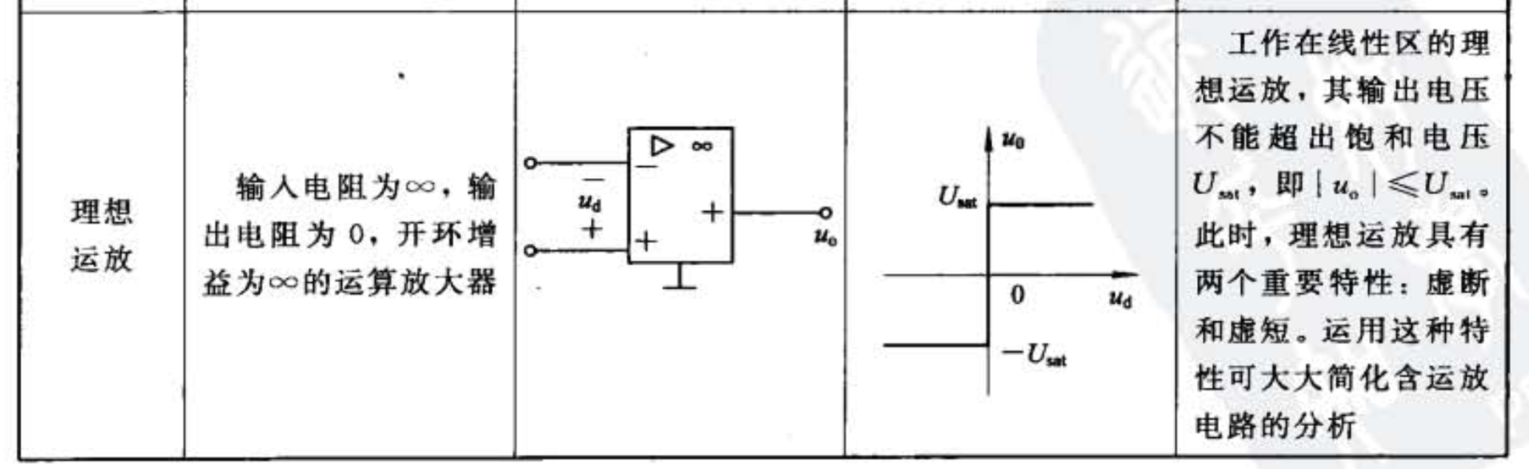
表示放大器的开环(差动)增益,运算放大器有很高的开环增益,理想运算放大器的开环增益为无穷大,一般为。
**开环组态 :**就算输入端的差动信号很小,仍然会让输出信号饱和,导致非线性的失真出现。因此运算放大器很少以开环组态出现在电路系统中,少数的例外是用运算放大器做比较器进行满幅输出,输出值通常为逻辑准位的“0”与“1”。
**负反馈组态 : **将运算放大器的反向输入端与输出端连接起来,放大器电路就处在负反馈组态的状况,此时通常可以将电路简单地称为闭环放大器。闭环放大器依据输入信号进入放大器的端点,又可分为反相(inverting)与非反相(non-inverting)两种。
闭环组态 :
反向闭环放大器-理想运放
- 开源增益无限大-->运放两输入端为虚接地,
- V-跟V+由于负反馈呈现虚短路(virtual short),导致此时V-等于V+
- 又因为输入阻抗无限大,此时I-跟I+均为零,此时自Vin到V-之电流Iin,等于V-到Vout之电流If
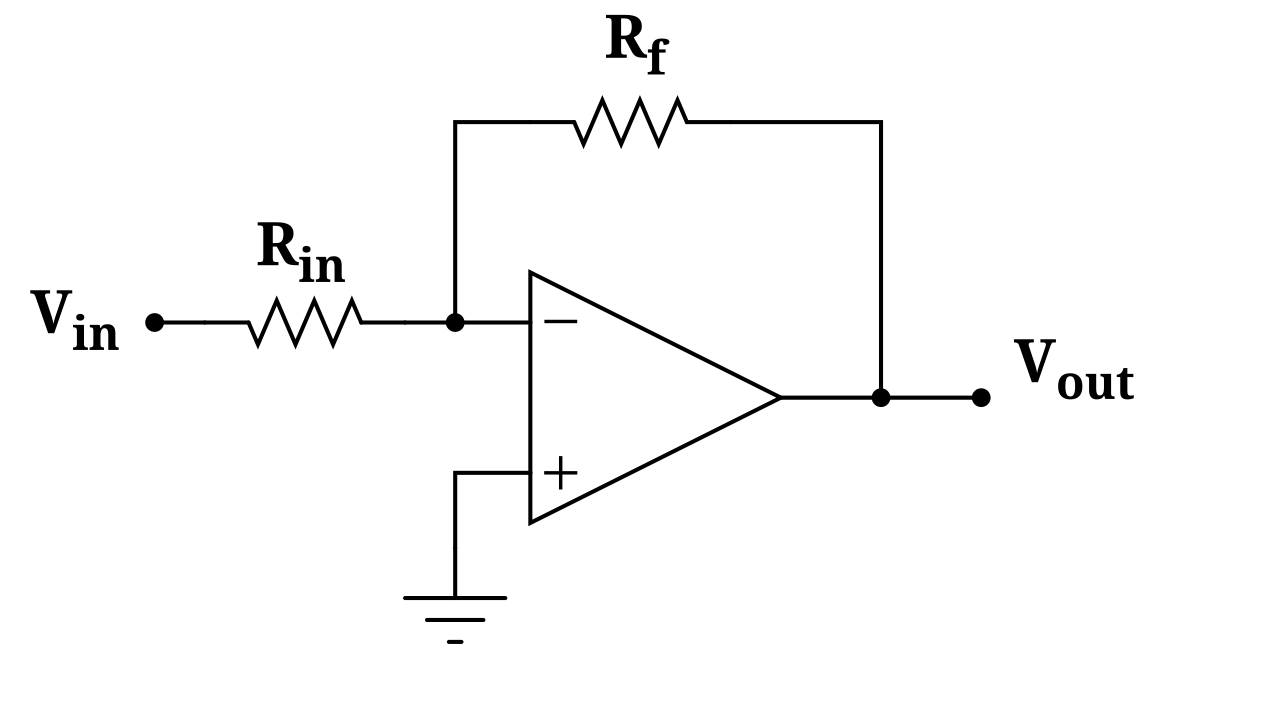
https://upload.wikimedia.org/wikipedia/commons/thumb/2/2d/Opampinverting.svg/1280px-Opampinverting.svg.png V_{out}=-\frac{R_f}{R_{in}}\times V_
- 开源增益无限大-->运放两输入端为虚接地,
**正相闭环放大器 : **
当运算放大器工作于线性(即非饱和)模式,非反相 (+) 端子和反相 (−) 端子是小到可以忽略的。
(+) 和 (−) 端子之间的输入阻抗比电路中任何其他电阻都大很多
https://upload.wikimedia.org/wikipedia/commons/thumb/6/66/Operational_amplifier_noninverting.svg/220px-Operational_amplifier_noninverting.svg.png
电路等效
完全相同的端口电压、电流关系(VCR),目的是简化电路的分析和计算。
等效电阻(不含独立源的二端电路)
电阻串并联
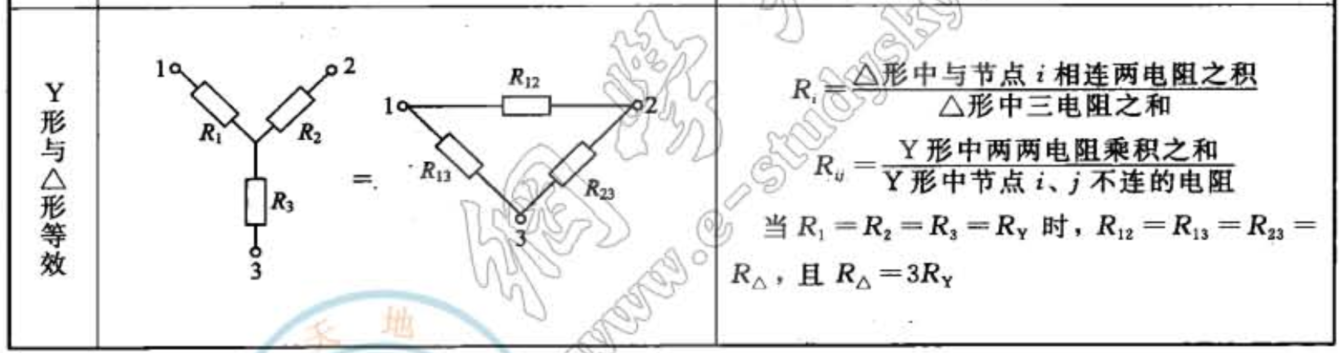
- Y形和Δ形等效
电源等效

- 无伴电压源转移、电流源转移
二、电阻电路分析
电路方程分析法:选取一组合适电路变量(电流或电压),根据基尔霍夫定律和元件的伏安关系,建立方程组并求解电路的方法统称方程分析法,也称一般分析法。
具有n个节点和b条支路的电路,其独立的KCL方程数为n-1,其对立的KVL方程数为b-n+1;
任选n-1个节点,所列出的KCL方程独立;对基本回路组或网孔列出的KVL方程独立
回路(电压)法
节点(电流)法
对于受控源的处理
电路定理
针对具体计算某条支路电压或电流时,电路定理更加简单
激励源:独立电压源或独立电流源(受控源不属于)
响应:电压或电流(功率不是响应)
- 齐次定理
- 叠加定理
- 替代定理
- 等效电源定理
- 最大功率传输定理
- 特勒根定理
- 互易定理
三、动态电路
**电路学习笔记33——一阶电路和二阶电路的时域分析:**https://www.bilibili.com/read/cv23498891/
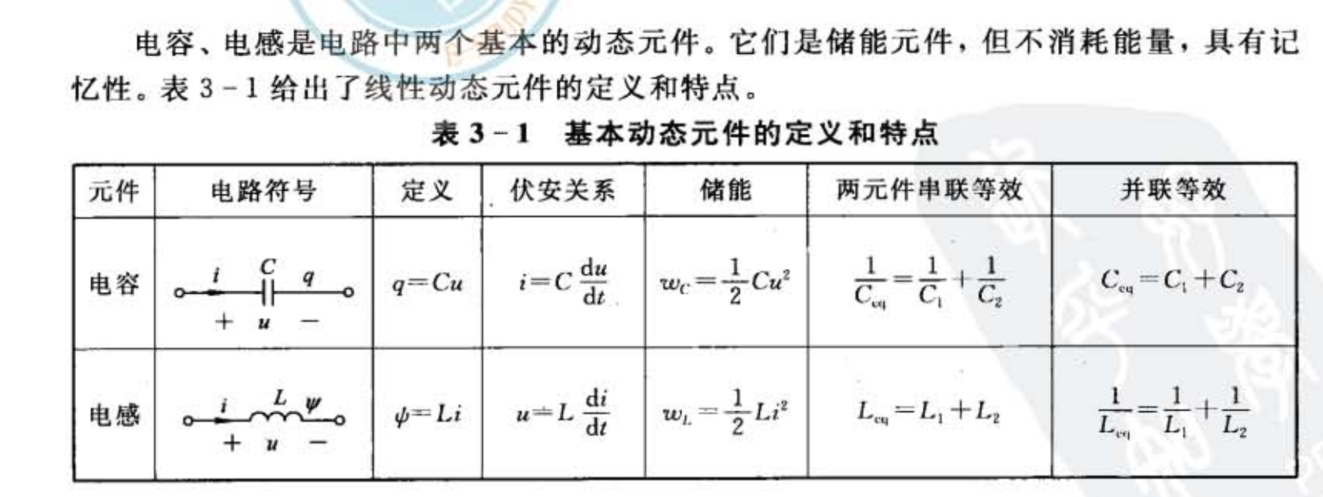
3.1 基本动态元件
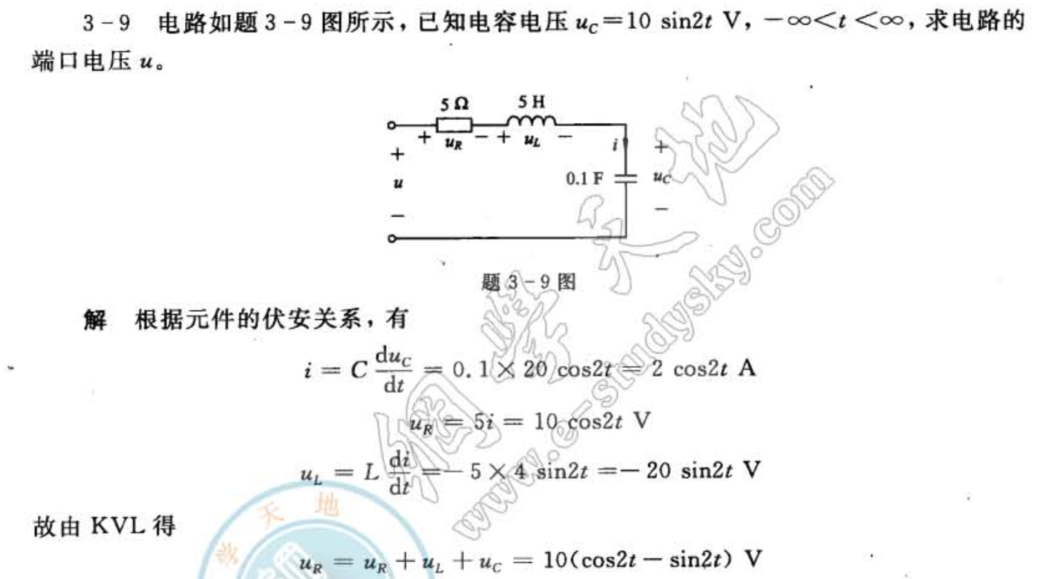
3.2 一阶动态电路分析
3.2.1 求解时刻响应的步骤
1.根据换路前时的电路,求出和
2.在电容电压、电感电流为有限值条件下,根据换路定律获得初始状态:
动态元件由于具有存储能量的作用,因此在电路的结构或元件的参数发生变化和换路时,其端电压和端电流是不能突然改变的。
在电路理论中这一性质可以表述为:当电容元件的初始电压为零或者电感元件的初始电流为零时,在换路的一瞬间,可以把电容元件看作短路,把电感元件看成开路。
强迫跃变是指?
3.换路后的电路中,用电压为的电压源替代电容,用电流为的电流源替代电感元件,得到等效电阻电路
4.利用电阻电路的分析方法,求所需时的初始值
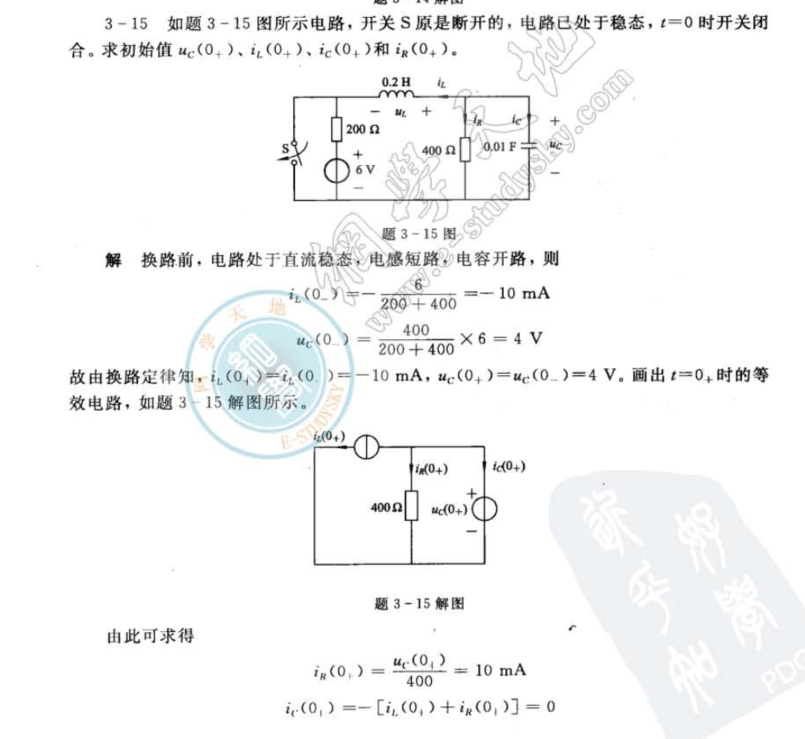
例子
3.2.2 三要素法

稳态值
电容在直流电路中相当于开路
电感在支路电路中相当于短路

3.3 全响应的分解
根据引起响应的起因:
- 零输入响应:指仅由电路的初始状态(即初始储能)引起的响应分量(此时电路的输入为零)。
- 零状态响应:初始状态为零时,仅由外部输入引起的响应分量。
根据响应的函数形式是否与外加输入有关考虑:
- 固有响应
- 暂态响应
- 稳态响应
- 强迫响应
3.4 阶跃函数与阶跃响应
3.5 二阶电路的零输入响应
四、正弦稳态分析
4.1 正弦量
按照正弦规律变化的电压、电流称为正弦电压、正弦电流,统称为正弦量。
式中,、、为正弦量的振幅,角频率和初相。
正弦量的有效值和振幅间的关系:
一般交流表意其读值均指有效值。
考虑相量表达形式,有
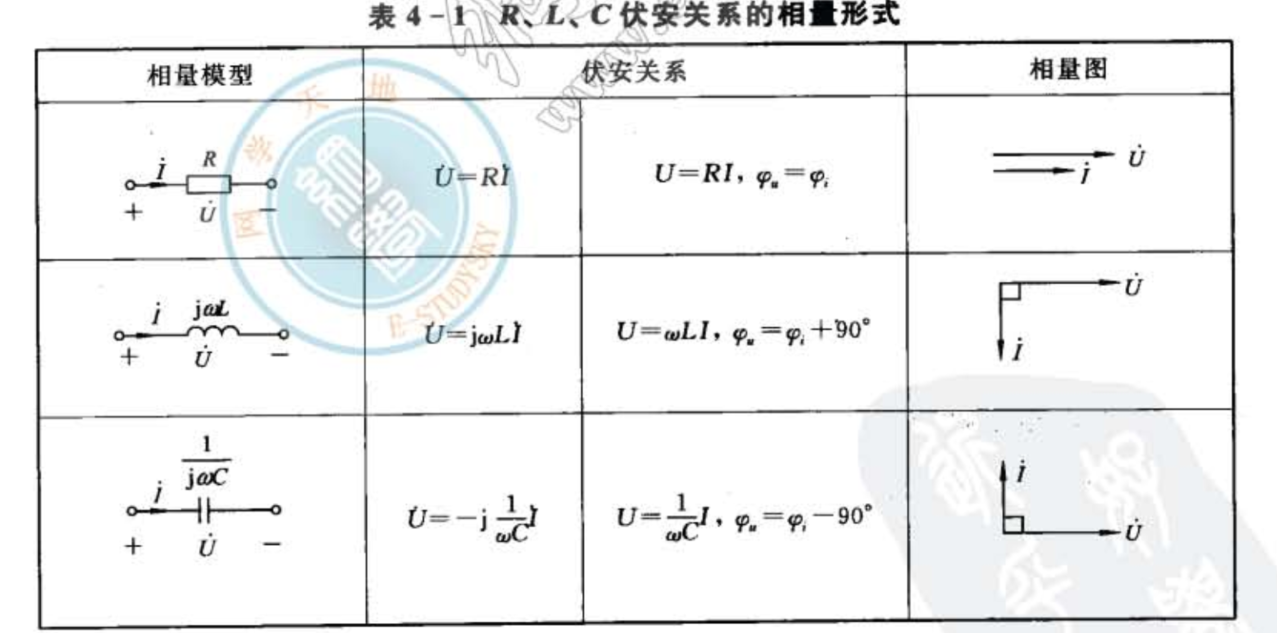
4.2 阻抗与导纳
4.3 正弦稳态电路的功率
相位差
- 有功功率 P
- 无功功率 Q
- 视在功率S
- 复功率
- 功率因数
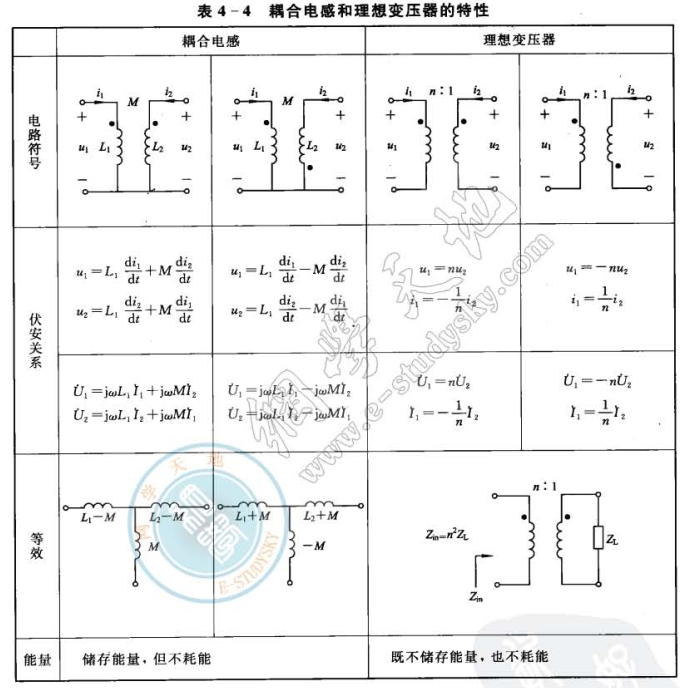
4.4 耦合电感与理想变压器
同名端:当电流从两线圈的某段子同时流入(或流出)时,若两线圈产生的磁通相助,则称此两端子为同名端,反之称为异名端。
耦合系数k: 衡量两线圈的耦合强弱
五、电路的频率响应和谐振现象
5.1 网络函数与频率响应
对于相量模型,在单一激励的情况下,将响应相量与激励相量之比定义为网络函数,即
- 幅频特性:,反映了响应与激励的振幅(或有效值)之比随频率变化的情况
- 相频特性:,反映了相位超前于激励的相位差随频率变化的情况。
电路的通(频)带、阻带,定义为的最大值
- 通带:一般定义为
- 阻带:反之则为
- 通、阻带边界频率称为截止频率(也称3 dB 频率 或 半功率点频率)
5.2 典型一阶RC电路的特性
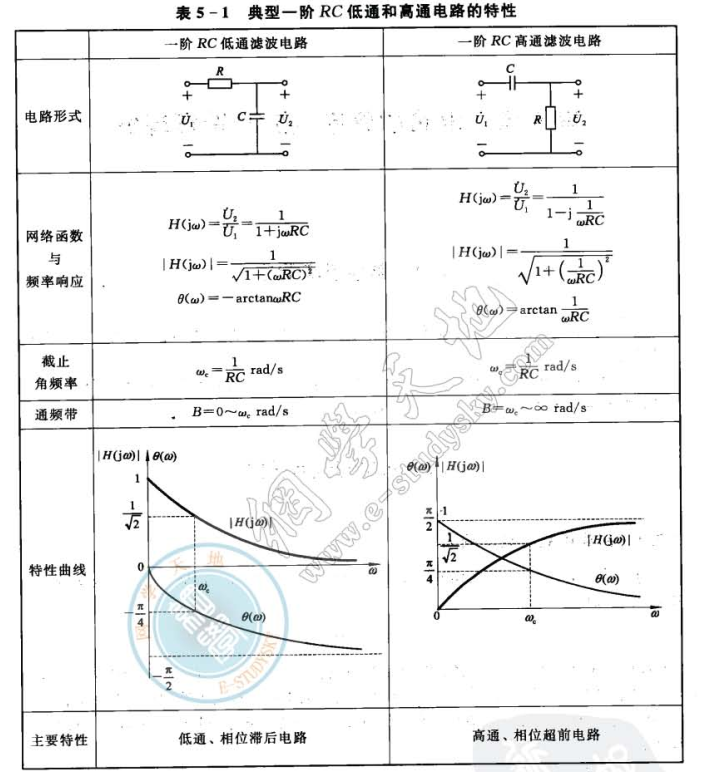
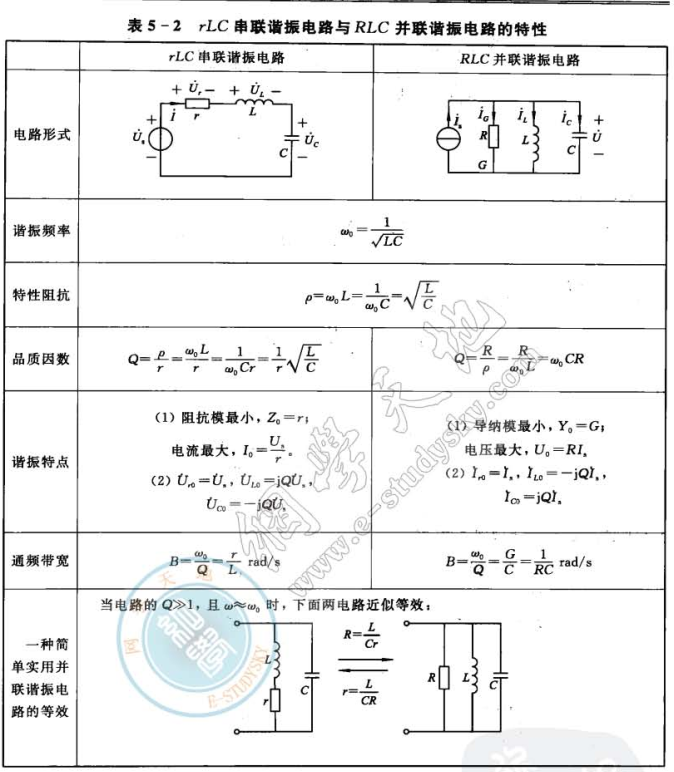
5.3 RLC电路的谐振
对于 二端 正弦 稳态 动态 电路 ,当端口电影呀和电流同向,则称该电路发生了谐振。
谐振条件: 二端口电路的等效阻抗为实数
六、二端口电路
6.1 参数方程
6.2 级联、串连、并联
6.3 网络函数
七、非线性电路
7.1 非线性元件
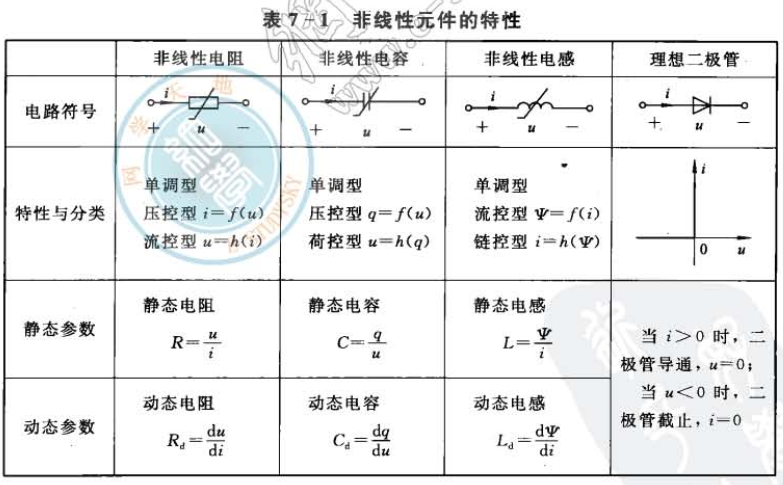
7.2 分析方法
仍利用KCL,KVL的元件的伏安关系建立电路方程。
非线性动态电路的方程是非线性微分方程,通常只能用计算器求出其数值解
图解分析法
小信号分析法
当电路中输入的交流信号的幅值相对于偏置直流电源的幅度足够小时,该交流信号通常称之为小信号
分段线性分析法